Chatbots and basic arithmetic

Prompting an LLM to write Python code to do simple math is more efficient and more accurate than having the LLM attempt to do the math itself

As LLMs (large language models) become increasingly sophisticated and resource-hungry, they continue to struggle with a certain type of task that can be performed efficiently on every single computer in existence: basic arithmetic. While modern computers can add, subtract, and multiply billions of times in the blink of an eye with perfect accuracy, these tasks frequently take chatbots substantially longer, and their answers are sometimes wrong.

On the other hand, modern LLMs are quite good at generating short segments of code in popular programming languages such as Python, and can therefore transform user requests to answer math problems into simple programs that perform the desired calculations. As it turns out, this approach can be substantially faster and more precise than allowing the LLM to attempt to perform the calculations itself.

import json
import ollama
import operator
import random
import sys
import time

LLM_MODEL = "llama3.1"
MATH_OPS = [
    (operator.add, " plus "),
    (operator.sub, " minus "),
    (operator.mul, " times ")
]


# generate a simple mathematical expression
def math_query (limit):
    arg1 = random.randint (0, limit)
    arg2 = random.randint (0, limit)
    op = random.choice (MATH_OPS) 
    return op[0] (arg1, arg2), str (arg1) + op[1] + str (arg2)
   

# basic Llama 3.1 chatbot
def llm_bot (text):
    convo = [{
        "role"    : "user",
        "content" : text
    }]
    response = ollama.chat (model=LLM_MODEL, messages=convo)
    message = response["message"]
    message["duration"] = response["total_duration"] \
        if "total_duration" in response else 0
    return message


def test (query):
    print ("========= QUERY =========")
    print (query[1])
    print ("========= CORRECT ANSWER =========")
    print (query[0])
    print ("========= LLM MATH =========")
    s = "What is " + query[1] + "?"
    print (s)
    response = llm_bot (s)
    print (response["duration"])
    print (response["content"])
    print ("========= LLM PYTHON =========")
    s = "Write a python program to calculate " + query[1] + \
            " and output the source code only"
    print (s)
    response = llm_bot (s)
    print (response["duration"])
    print (response["content"])


if __name__ == "__main__":
    iterations = int (sys.argv[1])
    limit = int (sys.argv[2])
    for i in range (iterations):
        test (math_query (limit))

For this experiment, the Llama 3.1 LLM (8B version) was used, run locally on a Macbook laptop via Ollama. The concept of the experiment is straightforward: 1000 randomly generated arithmetic problems (integer addition, subtraction, and multiplication) were submitted to the LLM in each of the following two forms:

• “what is X times Y?”

• “write a Python program to calculate X times Y and output the source code only”

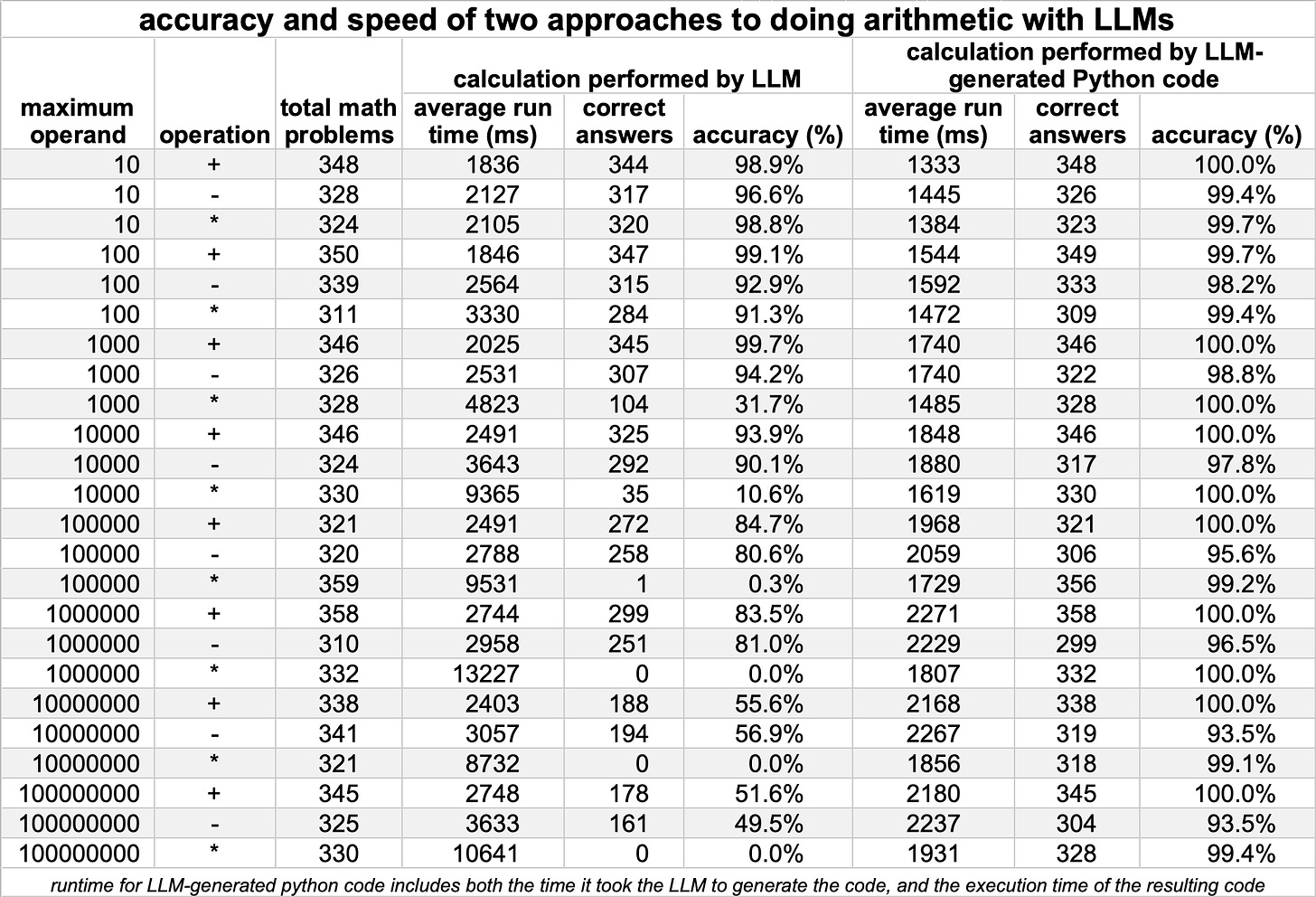
The operands X and Y are random positive integers. The above code generates the random math problems and outputs the correct answer, along with the LLM’s response to both prompts, and the time it took to generate each. The experiment was run eight times, using integers ranging from 0 to 10 the first time, 0 to 100 the second, and so on, increasing the maximum value by a factor of 10 each time.

# WARNING - SHITTY POSTPROCESSING CODE

import pandas as pd
import subprocess
import sys
import time


OPS = {
    "plus"  : "+",
    "minus" : "-",
    "times" : "*"
}

COLUMNS = {
    "CORRECT ANSWER" : "correct_result",
    "LLM MATH"       : "llm_math",
    "LLM PYTHON"     : "llm_python"
}


def read_file (fname):
    with open (fname, "r") as f:
        return f.read ()
    

def last_number (s):
    s = s.replace (",", "")
    t = s.split ()
    t.reverse ()
    for u in t:
        try:
            return int (u.replace (".", "").replace ("*", ""))
        except:
            pass
    return None


def execute (code):
    with open ("_tempcalc.py", "w") as f:
        f.write (code)
    try:
        output = subprocess.check_output (["python3", "_tempcalc.py"])
        try:
            return last_number (output.decode("utf-8"))
        except:
            code = code + ("\nprint (result)")
            with open ("_tempcalc.py", "w") as f:
                f.write (code)
            try:
                output = subprocess.check_output (["python3",
                    "_tempcalc.py"])
                try:
                    return last_number (output.decode("utf-8"))
                except:
                    return None
            except subprocess.CalledProcessError as err:
                return None
    except subprocess.CalledProcessError as err:
        return None
    

files = sys.argv[1:]
items = []
for file in files:
    rows = []
    data = read_file (file)
    data = data.split ("========= QUERY =========")
    for s in data:
        s = s.strip ()
        if len (s) > 0:
            t = s.split ("========= ")
            query = t[0].strip ()
            row = {"query" : query}
            for s in t[1:]:
                u = s.split ("=========")
                row[COLUMNS[u[0].strip ()]] = u[1].strip ()
            row["type"] = OPS[query.split ()[1]]
            lmath = row["llm_math"]
            row["llm_result"] = last_number (lmath) 
            lr = lmath.split ("\n")
            row["llm_query"] = lr[0]
            row["llm_time"] = float (lr[1]) / 1000000
            lpython = row["llm_python"]
            py = lpython[lpython.find ("```") + 3:]
            py = py[:py.find ("```")] if "```" in py else py
            py = py.strip ()
            if py.startswith ("python"):
                py = py[6:].strip ()
            if "`" in py:
                py = py[py.find ("`") + 1:]
                py = py[:py.find ("`")]
            row["python"] = py
            ptime = time.time ()
            row["python_result"] = execute (py)
            ptime = (time.time () - ptime) * 1000
            lr = lpython.split ("\n")
            row["llm_query_python"] = lr[0]
            row["llm_time_python"] = float (lr[1]) / 1000000 + ptime
            rows.append (row)
    df = pd.DataFrame (rows)
    df["correct_result"] = df["correct_result"].astype (int)
    print ("file: " + file)
    print ("total rows: " + str (len (df.index)))
    print ()
    for op in "+-*":
        df0 = df[df["type"] == op]
        total = len (df0.index)
        lcount = len (df0[df0["correct_result"] == \
                df0["llm_result"]].index)
        ltime = df0["llm_time"].mean ()
        print (op + " (math performed by LLM):                       " \
                + str (lcount) + " / " + str (total) + " = " + \
                str (int (lcount * 1000 / total) / 10) + \
                "% \t average runtime " + \
                str (int (ltime)) + " ms")
        pcount = len (df0[df0["correct_result"] == \
                df0["python_result"]].index)
        ptime = df0["llm_time_python"].mean ()
        print (op + " (math performed by LLM-generated python code): " \
                + str (pcount) + " / " + str (total) + \
                " = " + str (int (pcount * 1000 / total) / 10) + \
                "% \t average runtime " + \
                str (int (ptime)) + " ms")
        items.append ({
            "file"           : file,
            "operation"      : op,
            "total"          : total,
            "llm_time"       : ltime,
            "llm_correct"    : lcount,
            "llm_acc"        : lcount / total,
            "llm_py_time"    : ptime,
            "llm_py_correct" : pcount,
            "llm_py_acc"     : pcount / total
        })
    print ("")
df = pd.DataFrame (items)
df.to_csv ("llm_py_math_summary.csv", index=False)

Next, the LLM output was parsed, and the Python code generated by the second prompt executed, with its execution time added to the time it took the LLM to generate the code. The results of both calculation methods were then compared with the correct answer, and the results tallied by mathematical operation (addition, subtraction, or multiplication) and maximum operand size (10¹ - 10⁸).

the LLM-only approach is worse than the code generation approach

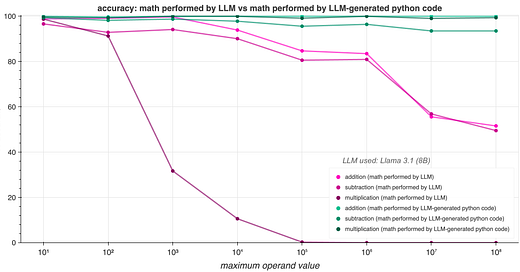
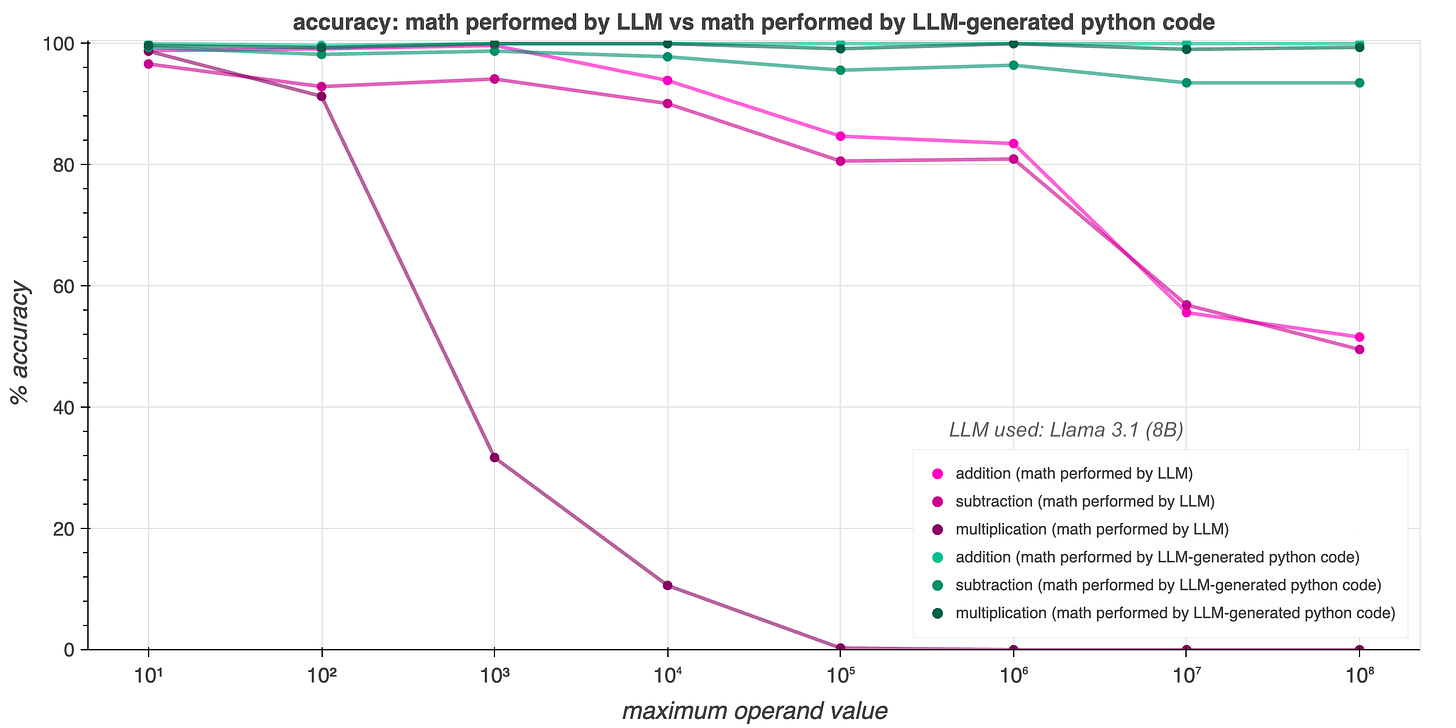
The result are summarized in the above table. Regardless of integer size or mathematical operation chosen, using the LLM to generate Python code to solve the math problem was both faster and more accurate than having the LLM attempt to solve the problem itself. The LLM-only approach was particularly unreliable at multiplication, with accuracy dropping below half when multiplying numbers between 1 and 1000, and to less than one percent when dealing with numbers between 1 and 100000. In contrast, accuracy for all operations remained above 93% for the code generation approach, regardless of operand size.

the LLM-only calculation method loses accuracy quickly as numbers grow

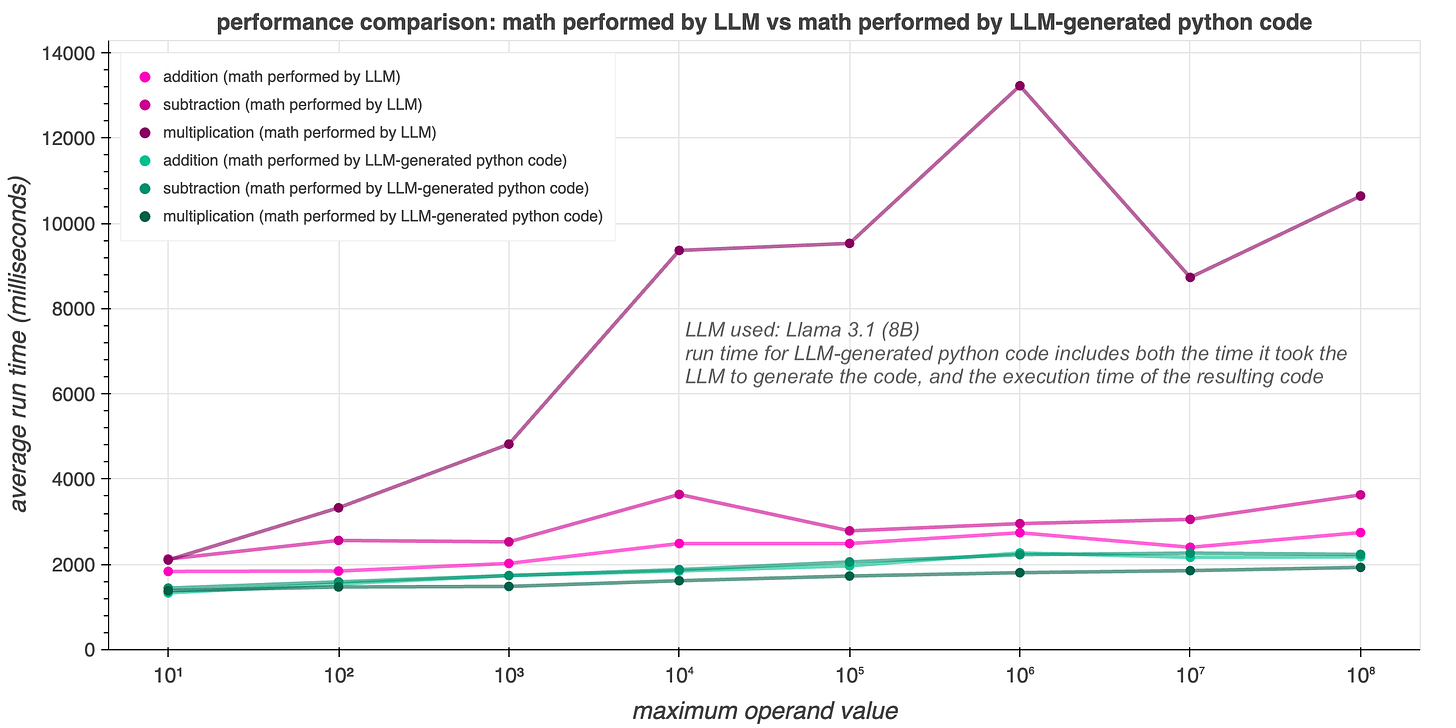
In addition to being less accurate, the LLM-only calculation approach was also slower than the code-generation approach. As with accuracy, this difference is particularly noticeable with multiplication, with the LLM-only method taking five times as long or more when dealing with larger numbers. (Note that the run time for the code-generation approach includes both the time spent by the LLM generating the code, and the execution time of the resulting Python program.)

the LLM-only calculation method is slower than the code generation method

This result isn’t surprising; after all, the whole reason computers were invented in the first place was to provide a fast and reliable way of performing calculations, and the simple Python programs generated by the LLM use this capacity for calculation directly. It is likely that the results generalize to other tasks that LLMs tend to be bad at, but which can be performed efficiently and precisely by writing simple programs in traditional languages, such as counting the R’s in “strawberry”. The efficiency and accuracy of LLM-based chatbots could potentially be boosted significantly for certain types of tasks by building this behavior into the bot, rather than attempting to solve these tasks at the language model level.